
| General information |
| Description |
| The purpose of this calculation is to obtain information about shear, bending moment, and deflection distribution over the length of a statically indeterminate (continuous) beam, which is under various transverse loads: couples, concentrated and linearly distributed loads. The result of calculation is represented by shear force, bending moment and deflection diagrams. Extreme values of these functions, as well as their values at the ends of each segment of the beam, are also calculated. In addition all main steps of the solution are represented by formulas. |
| Assumptions |
|
|
|
|
| Sign conventions |
| Coordinate system has an origin on the left side of the beam. In Figures 1-3 all components are shown as positive. Clockwise external moments, downward forces, upward deflections are considered positive. Reaction is positive if it acts upward. Positive bending moment compresses the upper part of the beam; positive shear force acts clockwise against the material (Fig. 1). |

|
| Figure 1. Sign conventions for shear force V and bending moment M. |
|
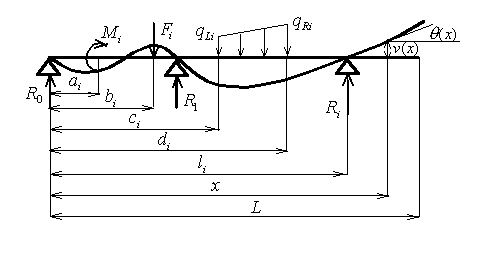
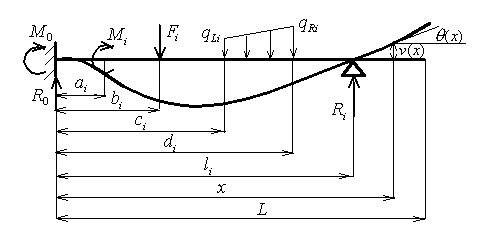
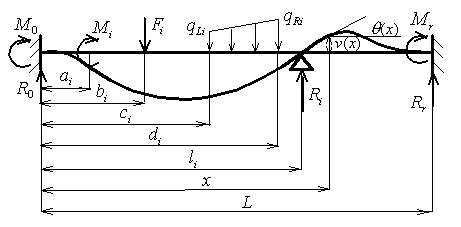
The left side of the beam could be simply supported or clamped.
The right end may be simply supported with or without overhang or clamped. The number of intermediate pin supports could be
arbitrary, but the beam must be statically indeterminate. For statically determined beams use another calculation.
|
|
|
|
| Figure 2. Beams with different types of edge conditions and loads. |
| Methodology |
|
At the first step of calculation we find the reactions using two equilibrium equations of the entire beam and geometrical equations corresponding to support conditions of the beam.
The equation of moment equilibrium about right support of the beam: |

|
| where l is the coordinate of the right support. In the case when the right end of the beam is clamped or simply supported without overhang l=L. In this and following formulas the linearly distributed load is divided into two parts. First one is the uniformly distributed load with intensity qLi and the second part corresponds to the distributed load whose left side intensity equals to 0 and the right one is equal to qRi- qLi. |
| The equation of beam equilibrium with respect to vertical axis: |

|
| For each pin support with coordinate li we have geometrical conditions: |

|
| If the left end of the beam is simply supported we have |

|
| For the clamped left end |

|
| For the clamped right end |

|
| Here v(x) and θ(x) are deflection and slope functions of the deformed beam. |
| Shear force and bending moment at a cross section located at distance x from the left end of the beam are obtained from equilibrium equations of free-body diagram of the left-hand part of the beam. |

|
| Figure 3. Free-body diagram of the left-hand part of the beam. |
| From the equation of vertical equilibrium we have the formula for shear force: |

|
| From the equation of moment equilibrium about right end point of the free-body diagram we obtain the formula for bending moment: |

|
| If the bending moment function M(x) is known, the deflection function v(x) could be found from the basic differential equation of the deflection curve of a prismatic beam: |

|
| After integration of this equation we obtain the formulas for deflection and slope functions: |

|

|
| where v0 and θ0 are deflection and slope of the deflection curve at x=0 respectively. In the case of simply supported or clamped left end of the beam v0 is equal to 0. We obtain the value of EIθ0 from other support conditions. For the clamped left end θ0=0. |
|
Note that in the above formulas only those members that correspond to the load components located to the left side of the considered cross section with coordinate x should be taken into account: values of ai, bi, ci, di, li must be less than x. Formulas can be simplified in the case of uniformly distributed load discarding members with factors (qRi- qLi), which are equal to 0. |
| References |
| James M. Gere, Stephen P. Timoshenko. Mechanics of Materials, PWS Publishing Co., 4th edition, 1997, 832 p. |