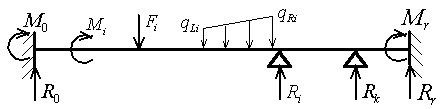Instructions - Bending of statically indeterminate (continuous) beams

Instructions

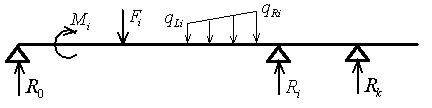
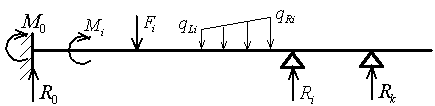
For calculation of reactions, shear forces, bending moments and deflections of statically indeterminate (continuous) beam, at the first step one has to choose the type of end conditions of the beam among the following cases:

The left side of the beam could be simply supported or clamped. The right end may be simply supported with or without overhang or clamped. The number of intermediate pin supports could be arbitrary, but the beam structure must be statically indeterminate. In the case of statically determined beam use another calculation.

Then the user has to enter the length of the beam L, number of pin supports (excluding left one), number of couples (external moments), concentrated and distributed loads, which are applied to the beam and submit these data. At the next steps user has to enter coordinates l_i of pin supports (excluding left one) in the increasing order and characteristics of each load: the values M_i and coordinates a_i of the external moments, the values F_i and coordinates b_i of the concentrated loads, left q_Li and right q_Ri values of the linearly distributed loads and corresponding left c_i and right d_i coordinates of the distributed loads. User should submit these data for each i-th load. For the uniform distributed load assume q_Li=q_Ri.

All coordinates must be positive and less then or equal to the length of the beam. According to the figures they are the distances of the load points from the left end of the beam. All load directions shown in the figures are positive. Use negative values when entering data for loads with the opposite directions.

There are no restrictions on the total number of loads and pin supports except the readability of the obtained result.

Please use the same system of units throughout the calculation. For instance, if you use force unit N and length unit m, the unit of distributed load and couple should be N/m and Nm respectively. Obviously, the result of calculation will have the same unit system in this case: shear force – N, bending moment – Nm.

The distribution of deflection along the length of the beam is represented by product EIv (whose unit will be Nm³ for our example), where E is elasticity modulus of material, I is moment of inertia of beam cross section about its neutral axis. Such representation of deflection is convenient when a beam is not designed yet and its properties are not defined. To obtain the deflection itself for the specific beam this result (EIv) should be divided by EI.

As a result you will obtain reactions, shear force, bending moment and deflection diagrams, extreme values of these functions as well as their values at the ends of each segment of the beam. In addition all steps of the solution will be represented by formulas.