Instructions
For calculation of the main characteristics of the structure, user has to enter the following data: the radius R of the sphere, the rise of the cap H, thickness of the shell h, which is constant in both directions, and material properties. It is assumed that the material of the shell is orthotropic with the elastic stress-strain relationship:

User has to enter the moduli of elasticity E1 and E2 of the material in meridional and circumferentional directions, as well as smaller Poisson’s ratio ν21. We assume that E2≥E1. This case corresponds to the structure reinforced mostly in the circumferential direction. The second Poisson’s ratio is calculated using formula (2). We check also the restriction (3) before the calculation.

Please use the same system of units throughout the calculation. For instance, if you use force unit N and length unit m, the unit of modulus of elasticity should be N/m2. Obviously, the result of calculation will have the same unit system in this case: deflection – m, load – N, stresses – N/m2.

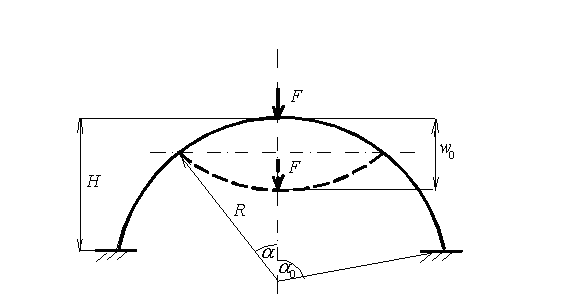
The program calculates the characteristics of the spherical structure in the following range of deflection amplitude 0<w0≤2H. We are focused on calculation of structure behavior by large deflections, therefore the following constraint is required: H≥0.1R.

Note that the calculated maximum bending stresses occur in the region of the shell, where the membrane stresses are equal to 0. Therefore the calculated maximum bending stresses are maximum main stresses of the structure.