| General information |
| Description |
| Thin isotropic elastic cylindrical shell subject to axial compression is considered. The response of the structure to local perturbations of different types (including lateral probing force, prescribed deflection, and energy barrier) is calculated. Special attention is paid to the energy barrier which is required for structure transition from initial equilibrium state to the post-buckling dimple-like state. Energy barrier criterion is used as a measure of metastability of the structure and applied for estimation of load level separating high and low sensitivity of the shell to the perturbations. It is shown that such axial load value relates to so called lower buckling load which is estimated in the calculation along with corresponding energy barrier. |

|
| Figure 1. Cylindrical shell under axial load with different types of boundary conditions (types of loading). |
| Assumptions |
|
|
| Methodology |
| It is shown that the transition of the shell from initial pre-buckling equilibrium state to post-buckling one requires energy barrier which is smallest in case of dimple-like mode. |

|
| Figure 2. Axially compressed cylindrical shells in post-buckling stages: (a) after local buckling; (b) after secondary general buckling. |
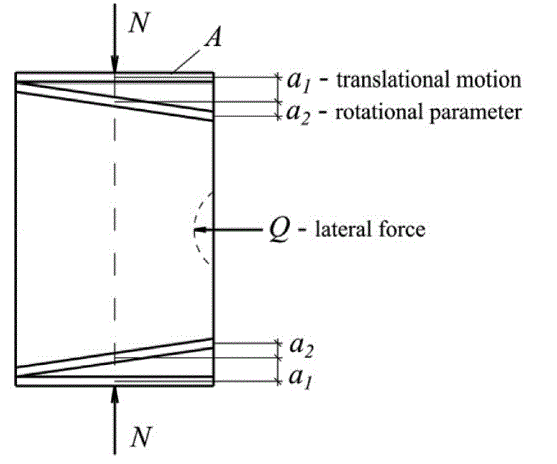
| In this case the assumption of classical theory that the axial load is uniformly distributed in circumferential direction along the edge of the cylinder is not valid for post-buckling stage. In our model the load is applied through rigid plates A (Fig. 1). Parameters a1 and a2 describe buckling translational motion and rotation of element A respectively. According to this approach, several types of boundary conditions (types of loading) were considered (see Table). Type 1 corresponded to free parallel displacement and rotation of the rigid elements. In this case two parameters a1 and a2 were defined in the model by equilibrium of elements A. The second type was characterized by rotation only, but parallel displacement of elements A was restricted. In the third type the rotation was restricted (a2= 0). Finally, a1= 0 and a2 = 0 in the fourth type, which is the case of pure rigid loading without rotation. The values 3, 2, 1, 0 of integer k (used in our model) are assigned to each loading type. The most practically important is Type 1. |

|
| After the following substitution for deflection w, force Q, total potential energy En and axial load N |

|
| the boundary value problem does not depend on shell parameters if deflections are less than shell thickness. If they are significantly greater, then the shell behavior depends mostly on Batdorf parameter |

|
|
Here R, L, h is radius, length and shell thickness, E, ν is modulus of elasticity and Poisson’s ratio of material,
U0 is deformation energy of the shell in the initial pre-buckling state,
Ncl is classical buckling pressure.
The analytical model is developed in the following research paper:
|

|
| Figure 3. Buckling and post-buckling behavior of axially compressed cylindrical shell under local perturbations: (a) lateral load 𝑄 deflection diagrams for different levels of axial load parameter 𝑁; (b) axial load deflection diagram. Here 𝑁- — lower local bucking load corresponds to minimum 𝑁 when post-buckling local equilibrium state exists, 𝑁+ — upper local bucking load corresponds to 𝑁 when the local post-buckling equilibrium state becomes unstable. |
|
The result is provided as Table of values of energy barrier En, maximum force Qmax,
deflection for the interval of axial load parameter N [0.3, 0.7]. Data are normalized according to above formulae.
Deflection amplitude w is normalized with respect to shell thickness h.
The graph of energy barrier depending on N is also depicted.
KDF corresponding to lower local buckling load along with energy barrier, deflection and buckling perturbation force Qmax is calculated. This value of KDF for one or several dimples can be used for estimation of design buckling axial load. |
|
If kn>=3 and Z>=400 the value of knockdown factor (KDF) for upper local buckling load N+ with corresponding energy barrier, delection amplitude, and buckling value of probing force Qmax is calculated as well. At the 4th type of loading k=0 and the load deflection diagram as well as lower local buckling load does not depend on number of buckles n. It depends only on Batdorf parameter. The energy barrier is proportional to n. In this case the KDF corresponding to lower buckling load can be well approximated as
For some comments or more information about calculation of nonlinear behavior of thin shells of different shapes and boundary conditions, geometrical and stiffness properties, and under different types of load please contact the author of the asymptotic method and present calculation Alex Yevkin by email and take a look at his personal web site. |
| References |
|