General information

Description

The buckling of thin simply supported orthotropic rectangular plate is considered. The plate is subject to uniformly distributed load Nx and Ny applied in the middle plane of the plate around its edges. The goal of calculation is to obtain the critical combination of the load. We obtain the solution of corresponding fourth-order partial differential equation with associated homogeneous boundary conditions. The minimum eigenvalue of the problem corresponds to the critical load. The solution is represented both graphically and as simple formulas.

Figure 1. Simply supported plate compressed in two directions by uniformly distributed load Nx and Ny.

Assumptions

The classical buckling theory of thin plate is applied.

The material of the structure is linear-elastic and orthotropic. The main directions of the orthotropy are parallel to the sides of the plate.

Methodology

We consider the orthotropic material with the following stress-strain relationship:

The boundary value problem for the deflection function w(x,y) is:

The stiffness coefficients in the differential equation are given by formulas

where h is the thickness of the plate.

The solution of this homogeneous boundary value problem is the deflection function

where n and m are natural numbers. Also we have equation

If Ny=0

Minimum of the critical load occurs when m=1 and

Similarly if Nx=0

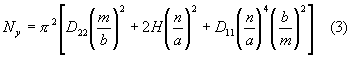
Minimum of Ny occurs when n=1 and

In general case for the given value of Nx one can find that

and minimum of Ny takes place if

Using last formulas we created algorithm for calculation of minimal critical load Ny for the different values of Nx.

References

S.P. Timoshenko and J.M. Gere. Theory of elastic stability, 2nd edition. McGraw-Hill, New York, 1961, 541 p. Robert M. Jones. Mechanics of composite materials, Taylor & Francis Inc., 2d edition, 1999, 519 p.. Laszlo P. Kollar, George S. Springer. Mechanics of composite structures, Cambridge University Press, 2003, 480 p.