General information

Description

Calculates internal forces of tension or compression in truss members of statically determinate 2D trusses under forces applied at arbitrary joints. All main steps of the solution are provided in each case. The method of joints is used in the calculation.

Assumptions

All members of truss, external forces, and reactions should be coplanar.

The number of members must be equal to 2*n-3, where n is the amount of truss joints.

All joints are hinged.

The total number of reactions (constraints) should be equal to 3 (one horizontal plus two vertical or one vertical plus two horizontal). They should be represented by their horizontal and vertical components and applied at joints.

External forces should be also applied at joints and represented by their horizontal and vertical components.

Coordinate system, sign conventions, and notations

Coordinate system has an origin on the left side and at the bottom of the truss (Fig. 1). The joint with number 1 is located at the origin of the coordinate system. Other joints have nonnegative coordinates. Vertical and horizontal components of reactions and external forces are considered as positive if they act toward the positive directions of corresponding coordinate axes. Internal forces of tension are considered as positive, but compressive forces are negative. For notation of vertical components of reactions and external forces we use letters V and Y respectively with the subscript corresponding to the number of joint where the force is applied. For horizontal components we use letters H and X. The internal force in a truss member is notated as Njk, where j and k are numbers of end joints of the truss member.

Figure 1. Truss diagram.

Methodology

For calculation of reactions we apply 3 equilibrium equations of entire truss: vertical and horizontal equilibrium equations

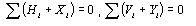
and equation of moment equilibrium about joint with number k

The order of consideration of equations and the number k are chosen by the condition that each equation should contain only one unknown reaction.

Figure 2. Free-body diagram of joint number j.

For calculation of internal forces we use the vertical and horizontal equilibrium equations of joints (Fig. 2):

where

We choose sequence of joint equilibrium equations, which contain the number of unknown internal forces corresponding to the number of equations.

References

Standard handbook of engineering calculations/ Tyler G. Hicks, editor; S. David Hicks, coordinating editor, - 3rd ed. McGraw-Hill, Inc, 1994, p. 1.12.