General information
Description
It is shown in [1] that in general case parameter estimation of g-renewal process is an ill-posed problem. It means that the obtained solution cannot be unique and it significantly depends on small changes in the input data. Previous numerical experiments have shown that the solution sometimes significantly depends on initial parameter values selected for the iteration methods and the process can converge to different local minimum (maximum) values. Therefore the calculation procedure requires a special sophisticated approach. Typically, additional information is required to resolve the ill-posed problem. It is suggested in [1] to solve the problem in two steps. At the first step, only underlying life time distribution function parameters are calculated using information about times of first failure of items. At the next step, all process parameters are calculated using all recurrent event times. Obviously, this approach not only converts ill-posed problem into a regular one, but also is very efficient in terms of computation time. Defining process parameters we used maximum likelihood estimator (MLE) [2]. For expected number of failures or cumulative intensity function (CIF) calculation we applied the advanced Monte Carlo method [3].

According to Kijima models we introduced virtual time yi after i-th failure

with restoration factor q and corresponding uptime xi. In addition we used scale parameter ai in the probability function to next failure
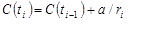
where eta and beta are parameters of underlying Weibull destribution function. We consider scale factor of two types
For graphical representation and comparison result we calculated CIF at each event time using non-parametric estimation. For this purpose we sorted all recurrence and censoring times (ages). If a recurrence age for an item is the same as its suspension age, then the recurrence time goes first. If multiple units have a common recurrence time, then they are shifted slightly, so that at any time only one event occurs. Then we calculated CIF using the following formula

where r=ri-1 if ti is recurrence time, r=ri-1-1 if ti is censoring time, r1=m, which is the total number of items in the test. Parameter a=1 in all cases except the case when ti corresponds to the very first failure in the test. In this case a=0.5. This value better fits the obvious condition CIF(t)≈F(t) for small CIF (according to non-parametric estimation for underlying failure probability function F(t)). Note that non-parametric estimation has its own error about 1/r.

We also studied the influence of Mean Time to Repair (MTTR) on CIF and Unavailability. This expansion of the model is especially important for imperfect repair because time to next failure is decreasing with the number of failures and therefore the influence of MTTR is increasing. The model yields good estimation of Unavailability at time greater than 3 mean times to repair.

1.V. Krivtsov and A. Yevkin ""Estimation of G-renewal process parameters as an ill-posed inverse problem"", Reliability Engineering & System Safety, Vol. 115, 2013, pp. 10-18.
2. A. Yevkin and V. Krivtsov "A generalized model for recurrent failures prediction", Reliability Engineering & System Safety, Vol. 204, 2020, 107125.
3. A. Yevkin. ""A Monte Carlo approach for evaluation of availability and failure intensity under g-renewal process model". In "Advances in Safety, Reliability and Risk Management". Proceedings of ESREL conference, France, Troyes, 2011, pp. 1015-1021.
4. A. Yevkin and nd V. Krivtsov "Modeling Recurrent Failure Processes using Padé Approximants". In Proceedings of RAMS 2025, USA, Florida, 2025.